Pythagoreische Tripel schnell berechnen

Pythagoreische Tripel

Eine beliebte Aufgabe für Programmieranfänger ist das Schreiben eines Programms zur Suche nach Pythagoreischen Tripeln. Das Programm soll also nach Lösungen für den Satz von Pythagoras a² + b² = c² finden, bei denen a, b und c natürliche Zahlen sind.

Ein Algorithmus, der alle Pythagoreischen Tripel für ein gegebenes c ausgibt, lässt sich leicht hinschreiben. Es genügt, nur solche Tripel auszugeben, bei denen a kleiner als b ist. Wir sind auch an Pythagoreischen Tripeln interessiert, bei denen der größte gemeinsame Teiler von a, b und c nicht 1 ist. In manchen anderen Betrachtungen wird sich nur auf solche, sogenannte Primitive Pythagoreische Tripel beschränkt.

Der Brute-Force Algorithmus

Hier also ein möglicher Code für diese Aufgabe in C++. Zunächst eine Hilfsfunktion isTripel() mit boolschem Rückgabewert, die dann true zurückgibt, wenn a, b und c eine Lösung des Satz von Pythagoras sind.

bool isTripel(int a, int b, int c)
{
  return a * a + b * b == c * c;
}


In der eigentlichen Funktion zur Berechnung aller Tripel für c ruft man diese Hilfsfunktion für alle a und b kleiner als c auf, das heißt in zwei verschachtelten Schleifen für a und für b. Da wir nur an Lösungen interessiert sind, bei denen a kleiner als b ist, können wir b in der inneren Schleife auch gleich bei a beginnen lassen.

void findTripel0_TwoNestedLoops(int c)
{
  for (int a = 1; a < c; ++a)
  {
    for (int b = a; b < c; ++b)
    {
      if (isTripel(a, b, c))
      {
        // Pythagoreisches Tripel a, b, c gefunden
      }
    }
  }
}


Probiert man diese Funktion nun für verschiedene c aus, stellt man fest: Mit wachsendem c wird sie schnell - langsamer. Wenn c kleiner als 500 ist, kommen die Ergebnisse noch in Sekundenbruchteilen. Für Werte von 10000 hingegen ist die Berechnung behäbig und benötigt Sekunden. Weil isTripel() (c-1)²/2-mal aufgerufen wird, die Funktion also quadratische Komplexität hat, ist dieses Laufzeitverhalten leicht zu erklären.

Tripel in Linearer Laufzeit

Wie kann man den Algorithmus so umformulieren, dass er nur noch lineare anstatt quadratische Komplexität hat? Wenn man für ein gegebenes a, b und c die Terme a * a + b * b und c * c vergleicht, wird sofort klar, dass das obige Verfahren eine Menge überflüssiger Tests durchführt. Denn falls gilt a * a + b * b > c * c, müssen für ein gegebenes a noch größere Werte als b nicht weiter betrachtet werden. Umgekehrt gilt, falls a * a + b * b < c * c, dass man für ein gegebenes b noch kleinere Werte als a nicht weiter untersuchen muss.

Wenn man also die Suche also mit dem kleinstmöglichem Wert für a, also 1, und dem größtmöglichem Wert für b, das heißt c-1, beginnt, führt dies zu dem folgenden Algorithmus:

int testTripel(int a, int b, int c)
{
  int aabb = a * a + b * b;
  int cc = c * c;
  if (aabb == cc)
    return 0;
  if (aabb < cc)
    return -1;
  return 1;
}

void findTripel1_OneLoop(int c)
{
  int a = 1;
  int b = c - 1;
  while (a < b)
  {
    int result = testTripel(a, b, c);
    if (result == 0)
    {
      // Pythagoreisches Tripel a, b, c gefunden
      ++a;
    }
    else if (result < 0)
    {
      ++a;
    }
    else
    {
      --b;
    }
  }
}


Wenn man ein Tripel gefunden hat, ist es im Grunde egal, ob a erhöht oder b erniedrigt wird. Hauptsache man verlässt das Paar (a,b) in die richtige Richtung. Schön ist an diesem Algorithmus auch die Abbruchbedingung a < b, die genau die vorher genannte Bedingung "Tripel [...], bei denen a kleiner als b ist" darstellt.

Dieser Algorithmus läuft, jedenfalls für größere c, um Größenordnungen schneller als der ursprüngliche Algorithmus. Tatsächlich stellt man bald fest, dass ein größerer Datentyp als int für a, b, und c und für die Zwischenergebnisse nötig sind. Für die folgenden Verbesserungen wird der 64-bit Integerdatentyp int64_t verwendet werden.

Inkrementelle Verbesserungen

Die Differenz der Quadratzahl a² zur nächsten Quadratzahl (a+1)² ist 2*a + 1, nach der ersten binomischen Formel. Ebenso ist die Differenz von b² zu (b-1)² gleich 2*b - 1. Damit kann man den Anfangswert von a * a + b * b vor Beginn der Schleife berechnen und dann inkrementell bei jeder Änderung von a und b anpassen. Zusätzlich kann man von diesem Anfangswert zu Beginn c * c abziehen. Dann reicht zur Prüfung, ob ein Pythagoreisches Tripel vorliegt, ein Vergleich des Werts mit 0. a muss erhöht werden, falls der Wert kleiner als 0 ist, andernfalls wird b vermindert.

void findTripel2_OneLoop(int64_t c)
{
  int64_t a = 1;
  int64_t b = c - 1;
  int64_t a2b2_c2 = a * a + b * b - c * c;
  while (a < b)
  {
    if (a2b2_c2 < 0)
    {
      a2b2_c2 += a + a;
      ++a;
    }
    else if (a2b2_c2 > 0)
    {
      a2b2_c2 -= b + b;
      --b;
    }
    else if (a2b2_c2 == 0)
    {
      // Pythagoreisches Tripel a, b, c gefunden
      a2b2_c2 += a + a;
      ++a;
    }
    ++a2b2_c2;
  }
}


Durch diese Änderungen gibt es - innerhalb der Schleife - keine Multiplationen mehr. Das sorgt für eine Beschleunigung um etwa den Faktor zwei.

Eine weitere Beschleunigung kann man durch die folgende Beobachtung gewinnen: für ein gerades c müssen für ein Pythagoreisches Tripel entweder a und b beide gerade, oder a und b beide ungerade sein. Ebenso müssen für ein ungerades c genau entweder a oder b ungerade sein. Damit reicht es aus, nur nach jeder zweiten Änderung von a bzw. b den Test auf ein Pythagoreisches Tripel durchzuführen. Natürlich muss man aufpassen, dass für die gewählten Anfangswerte von a und b bei dem ersten Test auf ein Tripel die Bedingungen für gerade und ungerade erfüllt sind. Für unsere Startwerte a = 1 und b = c - 1 ist das aber der Fall. Damit verändert sich der Algorithmus zu:

void findTripel3_OneLoop(int64_t c)
{
  int64_t a = 1;
  int64_t b = c - 1;
  int64_t a2b2_c2 = a * a + b * b - c * c;
  while (a < b)
  {
    if (a2b2_c2 == 0)
    {
      // Pythagoreisches Tripel a, b, c gefunden
    }

    a2b2_c2 += a + a + 1;
    ++a;

    if (a2b2_c2 < 0)
    {
      a2b2_c2 += a + a;
      ++a;
    }
    else
    {
      a2b2_c2 -= b + b;
      --b;
    }
    ++a2b2_c2;
  }
}


Die Änderung sorgt nur für eine kleine Geschwindigkeitsverbessung. Sie erlaubt aber die folgende weitere Verbesserung: In dem obigen Algorithmus werden alle Operationen in der inneren Schleife auf a2b2_c2 - die Additionen und Subtraktionen von a, von b und von 1 - zweimal durchgeführt. Stattdessen kann man diesen Wert anfangs halbieren, und dann jede Addition nur einmal durchführen. Die Halbierung funktioniert nur, weil der Anfangswert von a2b2_c2 in jedem Fall gerade ist, egal, ob a und b ungerade oder gerade sind.

Der Anfangswert mit diesen Veränderungen ist also (a * a + b * b - c * c) / 2. Insgesamt verändert sich der Algorithmus wie folgt:

void findTripel4_OneLoop(int64_t c)
{
  int64_t a = 1;
  int64_t b = c - 1;
  int64_t a2b2_c2 = (a * a + b * b - c * c) / 2;
  while (a < b)
  {
    if (a2b2_c2 == 0)
    {
      // Pythagoreisches Tripel a, b, c gefunden
    }

    a2b2_c2 += a + 1;
    ++a;

    if (a2b2_c2 < 0)
    {
      a2b2_c2 += a;
      ++a;
    }
    else
    {
      a2b2_c2 -= b;
      --b;
    }
  }
}


Durch die verringerte Anzahl an nötigen Operationen ist diese Variante des Algorithmus mit linearer Laufzeit nochmals etwa 30 Prozent schneller als die vorige. Verglichen mit dem Ursprungsalgorithmus mit linear Laufzeit beträgt der Vorsprung mehr als das dreifache. Rein optisch wirkt der Algorithmus jetzt sehr aufgeräumt und auf das Minimum reduziert. Allerdings ist keineswegs mehr so offensichtlich, was dieser Algorithmus berechnet und wie er funktioniert. Ist man an selbst-dokumentierenden Quellcode interessiert, ist diese letzte Optimierung nicht hilfreich.

Tripel in geringerer als Linearer Laufzeit

Mit den Änderungen im letzten Abschnitt scheint das Ende der Fahnenstange für die Geschwindigkeitsoptimierung des Linearen Algorithmus erreicht. Für eine weitere Verbesserung braucht es eine neue Idee.

Diese Idee liefert der Wikipedia-Artikel:

Die Formeln

      a = u * u - v * v
      b = 2 * u * v
      c = u * u + v * v

liefern für beliebige natürliche Zahlen u und v mit u > v ein pythagoreisches Tripel. Es ist genau dann primitiv, wenn u und v teilerfremd und nicht beide ungerade sind. Bereits Euklid hat diese Formeln angegeben.

Damit könnte ein Algorithmus zur Berechnung von primitiven Pythagoreischen Tripeln so aussehen:

void findPrimitiveTripel(int64_t c)
{
  int64_t sqrtc = static_cast(std::sqrt(c));

  for (int64_t v = 1; v < sqrtc; ++v)
  {
    for (int64_t u = v + 1; u <= sqrtc; ++u)
    {
      if (v * v + u * u == c)
      {
        if (ggt(u, v) == 1 &&
          (v + u & 1) == 1)
        {
          // Pythagoreisches Tripel a: u*u - v*v, b: 2*u*v, c gefunden
        }
      }
    }
  }
}


Der Algorithmus ist sehr ähnlich zum ersten Algorithmus mit zwei verschachtelten Schleifen. Es wird über v und u iteriert, wobei durch den Startwert von u = v + 1 in der inneren Schleife die Bedingung u > v implizit sichergestellt wird. Falls nun v * v + u * u == c gilt, werden noch die zusätzlichen Bedingungen für die Teilerfremdheit (ggt(u, v) == 1) und dass u und v nicht beide ungerade sind ((v + u & 1) == 1) geprüft. Bei dem letzten Check wird ausgenutzt, dass wenn u und v beide gerade sind, der ggt ein Vielfaches von 2 ist, und somit dieser Fall nicht extra geprüft werden muss. Damit genügt es, zu testen, ob v + u ungerade ist.

Nun war unsere Ausgangsfrage, nach allen Pythagoreischen Tripeln für ein gegebenes c zu suchen, also auch nach nicht primitiven. Das heißt, wir suchen nach Tripeln der Form m * a * a + m * b * b = m * c * c, wobei dann a, b und c ein primitives Tripel bilden. Damit können wir den Algorithmus von eben abwandeln, so dass er die primitiven Tripel für c / m sucht, und dann das m-fache ausgibt.

void findMultipleOfPrimitiveTripel0_TwoNestedLoops(int64_t c, int64_t m)
{
  int64_t sqrtc = static_cast(std::sqrt(c / m));

  for (int64_t v = 1; v < sqrtc; ++v)
  {
    for (int64_t u = v + 1; u <= sqrtc; ++u)
    {
      if (v * v * m + u * u * m == c)
      {
        if (ggt(u, v) == 1 &&
          (v + u & 1) == 1)
        {
          // Pythagoreisches Tripel a: m * (u*u - v*v), b: m*2*u*v, c gefunden
        }
      }
    }
  }
}


Um alle Tripel für c zu finden, muss diese Funktion für Teiler m von c aufgerufen werden. Man könnte sich auf manche m beschränken, aber es ist nicht ganz leicht zu sehen, welche m benötigt werden. Im folgenden Code wird die Funktion daher für alle Teiler m aufgerufen. Wenn ein Tripel gefunden wurde, ist daher noch eine zusätzliche Prüfung nötig, ob es sich um schon vorher gefundenes Tripel haldelt. Die Tripel sind bei dieser Methode ohnehin nicht nach a sortiert, darum sollten sie ohnehin vor der Ausgabe sortiert werden.

std::vector findDivisors(int64_t c)
{
  std::vector divisors;

  int64_t mLimit = static_cast(std::sqrt(c));
  for (int64_t m1 = 1; m1 <= mLimit; ++m1)
  {
    if (c % m1 != 0)
      continue;
    int64_t m2 = c / m1;

    divisors.push_back(m1);
    if (m2 != m1)
      divisors.push_back(m2);
  }

  return divisors;
}

void findTripelEuklid(int64_t c)
{
  auto divisors = findDivisors(c);
  for (int64_t m : divisors)
  {
    findMultipleOfPrimitiveTripel(c, m);
  }
}


Diese Algorithmus hat zunächst ähnliche Laufzeit wie die im vorigen Abschnitt, also linear. Aber: Es sind für diesen Algorithmus die gleichen Verbesserungen möglich wie für den ersten Algorithmus mit den zwei verschachtelten Schleifen.

Insbesondere kann man auf die gleiche Weise den Algorithmus formulieren, so dass er nur eine Schleife benötigt.

void findMultipleOfPrimitiveTripel1_OneLoop(int64_t c, int64_t m)
{
  int64_t sqrtc = static_cast(std::sqrt(c / m));

  int64_t v = 1;
  int64_t u = sqrtc;
  while (v < u)
  {
    int64_t v2mu2m = v * v * m + u * u * m;
    if (v2mu2m == c)
    {
      if (ggt(u, v) == 1 &&
        (v + u & 1) == 1)
      {
        // Pythagoreisches Tripel a: m * (u*u - v*v), b: m*2*u*v, c gefunden
      }
      ++v;
    }
    else if (v2mu2m < c)
    {
      ++v;
    }
    else
    {
      --u;
    }
  }
}


Diese Änderung ist der Schritt, mit dem die Gesamtlaufzeit des Algorithmus geringer als linear wird. Die weiteren Optimierungen des naiven Algorithmus lassen sich ebenso anwenden: Die Quadratzahlen v*v und u*u lassen sich inkrementell berechnen:

void findMultipleOfPrimitiveTripel2_OneLoop(int64_t c, int64_t m)
{
  int64_t cDivm = c / m;
  int64_t sqrtc = static_cast(std::sqrt(cDivm));

  int64_t v = 1;
  int64_t u = sqrtc;
  int64_t v2u2_c = v * v + u * u - cDivm;

  while (v < u)
  {
    if (v2u2_c < 0)
    {
      v2u2_c += v + v;
      ++v;
    }
    else if (v2u2_c > 0)
    {
      v2u2_c -= u + u;
      --u;
    }
    else if (v2u2_c == 0)
    {
      if (ggt(u, v) == 1 &&
        (v + u & 1) == 1)
      {
        // Pythagoreisches Tripel a: m * (u*u - v*v), b: m*2*u*v, c gefunden
      }
      v2u2_c += v + v;
      ++v;
    }
    ++v2u2_c;
  }
}


Nur jede zweite Wert von v2u2_c muss überprüft werden. Im Unterschied zu dieser Optimierung im ursprünglichen Algorithmus muss in diesem Fall ausgenutzt werden, dass bei einem primitiven Pythagoreischen Tripel c immer ungerade ist. Damit ist also entweder a oder b ungerade, und die Startwerte von v und u können demnach so gewählt werden, dass u oder v gerade sind.

void findMultipleOfPrimitiveTripel3_OneLoop(int64_t c, int64_t m)
{
  int64_t cDivm = c / m;
  if ((cDivm & 1) == 0)
    return;

  int64_t sqrtc = static_cast(std::sqrt(cDivm));

  int64_t v = 1;
  int64_t u = sqrtc;
  if ((u & 1) != 0)
    ++u; // ensure that u + v is not even
  int64_t v2u2_c = v * v + u * u - cDivm;

  while (v < u)
  {
    if (v2u2_c == 0)
    {
      if (ggt(u, v) == 1)
      {
        // Pythagoreisches Tripel a: m * (u*u - v*v), b: m*2*u*v, c gefunden
      }
    }

    v2u2_c += v + v + 1;
    ++v;

    if (v2u2_c < 0)
    {
      v2u2_c += v + v;
      ++v;
    }
    else
    {
      v2u2_c -= u + u;
      --u;
    }
    ++v2u2_c;
  }
}


Schließlich kann auch in diesem Fall die Umformung des Algorithmus zu weniger Rechenoperationen durchgeführt werden. Das heißt, der Startwert von v2u2_c wird halbiert, und in der Schleife werden nur noch v bzw. u anstatt v+v bzw. u+u addiert.

void findMultipleOfPrimitiveTripel4_OneLoop(int64_t c, int64_t m)
{
  int64_t cDivm = c / m;
  if ((cDivm & 1) == 0)
    return;

  int64_t sqrtc = static_cast(std::sqrt(cDivm));

  int64_t v = 1;
  int64_t u = sqrtc;
  if ((u & 1) != 0)
    ++u; // ensure that u + v is not even
  int64_t v2u2_c = (v * v + u * u - cDivm) / 2;

  while (v < u)
  {
    if (v2u2_c == 0)
    {
      if (ggt(u, v) == 1)
      {
        // Pythagoreisches Tripel a: m * (u*u - v*v), b: m*2*u*v, c gefunden
      }
    }

    v2u2_c += v + 1;
    ++v;

    if (v2u2_c < 0)
    {
      v2u2_c += v;
      ++v;
    }
    else
    {
      v2u2_c -= u;
      --u;
    }
  }
}


Abschlussbetrachtung

Bei genauerer Untersuchung der Geschwindigkeit des letzten Algorithmus' bemerkt man, dass der Großteil der Laufzeit für die Bestimmung der Teiler von c benötigt wird. In der entsprechenden Methode gibt es noch viel Optimierungspotential. Effizienter als der angegebene Brute-Force Ansatz ist es, die Primfaktoren von c zu bestimmen und damit alle Teiler von c anzugeben. Durch so eine Verbesserung ist nochmals eine Beschleunigung um eine Größenordnung möglich.

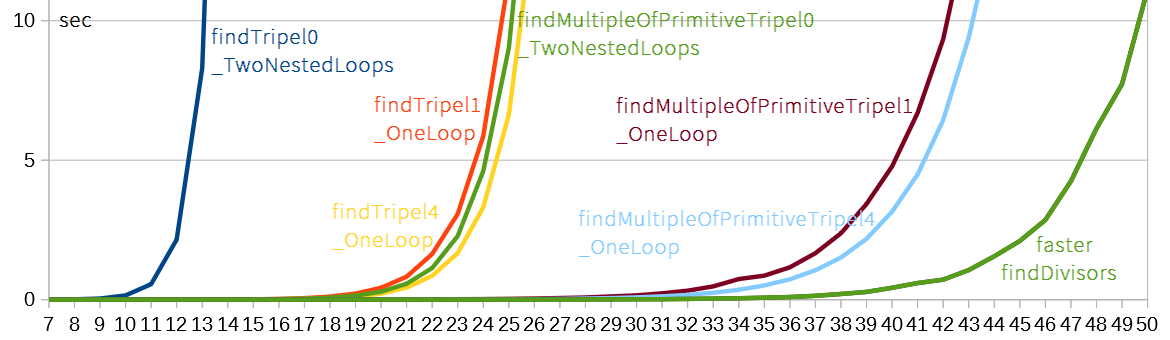
Diese Grafik zeigt die Laufzeit der verschiedenen Algorithmen für verschieden große Zahlen. Gemessen wurde jeweils die Zeit in Sekunden (aufgetragen auf der y-Achse) zur Berechnung aller Tripel zwischen c = 2^x und c = 2^x + 127. Man erkennt leicht den naiven Algorithmus mit quadratischer Laufzeit (die Kurve links), die verschiedenen Algorithmen mit linearer Laufzeit (Kurven in der Mitte) und die verschiedenen Algorithmen mit sub-linearer Laufzeit (auf der rechten Seite). Man sieht insbesondere, dass für c im Milliarden- bis in den Billionen-Bereich die Suche nach Pythagoreischen Tripeln in vernünftiger Zeit möglich ist, wenn man einen Algorithmus mit geringerer als linearer Laufzeit verwendet. Andererseits kann man erahnen, dass für c kleiner als etwa 2¹⁶ es noch keinen großen Unterschied macht, ob man einen Algorithmus mit linearer oder geringerer Laufzeit verwendet.